Bol Loops of Order 16 with Centrum of Size 4

As part of my enumeration of the Bol loops of order 16 with nontrivial centre, here I list just the 274 loops which are non-associative with centrum of size 4. Please see the parent page for notation, including my conventions for naming of loops and table entries. I would appreciate an email message () from you if you have any comments regarding this list.

3 loops in this category have |Z(L)|=1, namely

• 2 loops with |I(L)|=7:     16.7.4.77,   16.7.4.78;   and
• 1 loop with |I(L)|=15:     16.15.4.5.

Also 36 loops in this category have |Z(L)|=4, namely

• 16 loops with |I(L)|=3:     16.3.4.0,   16.3.4.1,   16.3.4.2,   16.3.4.3,   16.3.4.4,   16.3.4.5,   16.3.4.6,   16.3.4.7,   16.3.4.12,   16.3.4.13,   16.3.4.14,   16.3.4.15,   16.3.4.16,   16.3.4.17,   16.3.4.24,   16.3.4.25;
• 14 loops with |I(L)|=7:     16.7.4.0,   16.7.4.1,   16.7.4.6,   16.7.4.7,   16.7.4.8,   16.7.4.9,   16.7.4.10,   16.7.4.11,   16.7.4.12,   16.7.4.13,   16.7.4.14,   16.7.4.15,   16.7.4.61,   16.7.4.75;
• 4 loops with |I(L)|=11:     16.11.4.0,   16.11.4.1,   16.11.4.2,   16.11.4.3;   and
• 2 loops with |I(L)|=15:     16.15.4.0,   16.15.4.1.

The remaining 235 loops found in this category all have |Z(L)|=2 and so the graph Comm(L) is defined. This graph is displayed as black-on-white if it has at most 10 edges; otherwise its complement (which has at most 10 edges) is displayed as white-on-black. In either case, isolated vertices are not displayed.

No.	Comm(L)	|I(L)|=1	|I(L)|=3	|I(L)|=5	|I(L)|=7	|I(L)|=9	|I(L)|=11	|I(L)|=13	|I(L)|=15
6				19, 23, 24		8, 12, 38, 39		2
14			37		47		12, 19
25			36		26, 39, 48, 65		9, 11, 30
34		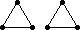	39		29, 62		26
38		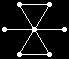		2, 3, 4, 5, 14		2
45		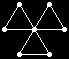	10, 11, 26		2, 3, 38, 66		7, 39
49			20		18, 19		4
50			31		24, 25, 43, 44, 50, 56, 73		20, 27, 28		3
58				17, 21, 40		24, 29, 33, 47		7
60		1		33, 35, 41		16, 18, 22, 28, 48, 49, 50		10
84			33		60, 68, 70		13, 18
86				15, 20, 25, 29, 32, 38		6, 7, 10, 31, 32, 34, 36, 43		1, 5
94		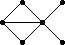		10, 16, 31, 44		0, 15, 37, 51, 54		3
100		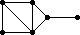	28, 29		31, 33, 37, 40, 53, 54, 55, 71		8, 10, 15, 17, 31, 35
120		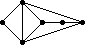	34		27, 41, 51, 63		14, 16, 36
143		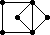	27		35, 59, 64		23, 37
147			8, 9	8, 9	4, 5
149			18, 40	0, 1, 6, 7, 12	16, 76	3
161			38		28, 46, 57		21, 33
165			35		32, 34, 36		24, 38
168				11, 37, 42, 43		1, 5, 13, 42, 53		0
176				26, 36		11, 17, 35		6
189		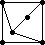			23, 49, 72				4
203		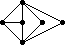		13		4
214		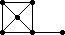		18, 22, 28		9, 14, 40, 41		4
218		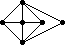	19		17, 20		5
219		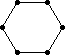	32		22, 30, 42, 52, 69		22, 25, 32		2
221		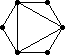2		30		21, 23, 25, 30, 46		9
225		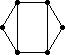	30		45, 58, 67		29, 34
236		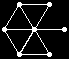0		27, 34, 39		19, 20, 26, 27, 44, 45, 52		8

/ revised November, 2001