Bol Loops of Order 16 with 1 Involution

As part of my enumeration of the Bol loops of order 16 with nontrivial centre, here I list just the 37 loops which are non-associative with exactly one involution. Please see the parent page for notation, including my conventions for naming of loops and table entries. I would appreciate an email message () from you if you have any comments regarding this list.

The isomorphism invariants indicated in our list suffice to distinguish all nonisomorphic pairs, with the exception of the following three pairs:

• Loops 16.1.2.0 and 16.1.2.5. These are distinguished as follows: Whenever x and y are non-commuting elements of order 8, the inner map L_x,y maps y−>y⁵ in loop 16.1.2.0, but maps y−>y³ in loop 16.1.2.5.
• Loops 16.1.2.2 and 16.1.2.3. These are distinguished as follows: Let x and y be non-commuting elements of order 8 such that x²=y². Then the inner map R_x,y maps y−>y⁻¹ in loop 16.1.2.2, but maps y−>y³ in loop 16.1.2.3.
• Loops 16.1.2.6 and 16.1.2.7. These are distinguished as follows: Let y be an element of order 8. Then there are eight elements x of order 4 not commuting with y. In loop 16.1.2.7, the inner map T_x maps y−>y³ in all cases; but in loop 16.1.2.6, there are four choices of x (for each y) such that T_x maps y−>y⁻¹.

All 37 loops in this list have |Z(L)|=2 and so the graph Comm(L) is defined. This graph is displayed as black-on-white if it has at most 10 edges; otherwise its complement (which has at most 10 edges) is displayed as white-on-black. In either case, isolated vertices are not displayed.

No.	Comm(L)	|C(L)|=2	|C(L)|=4
1	empty graph	31
5		30
10		33
12		29
13		34
18		6, 7
21		12
33		0, 2, 3, 5, 32
42		15
51		16
60			1
69		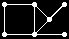20
79		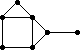11
97		19
102		10
133		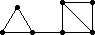9
148		25
151		26
153		14
155		23
171		1, 4
186		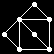17
188		13
190		28
192		18
198		21
220		27
221		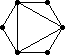	2
228		22
236		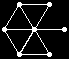	0
243		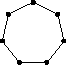24

/ revised November, 2001