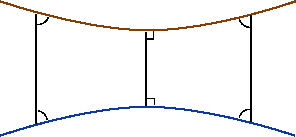
A negatively curved surface appears (to an ant on the surface) like a mountain pass or saddle: one sees the surface veer upwards on the left and right, but downwards to the front and back.

Geodesics on a negatively curved surface tend to veer apart from each other. Two non-intersecting geodesics are shown. Note that the geodesics have a common perpendicular, representing the shortest distance between points of the two geodesics.

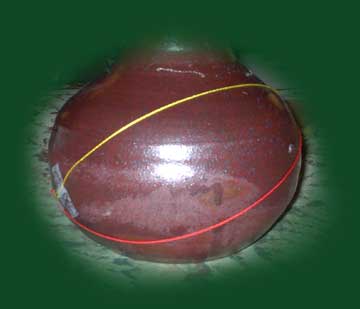
A surface of zero Gaussian curvature (such as the cylinder shown) has the property that regions on the surface may be represented by planar maps which perfectly represent both distances (with a scale factor) and angles.

Geodesics on a surface of zero curvature behave just as in a plane; either they intersect (as do lines in a plane) or they are parallel, as shown. Note that parallel geodesics stay the same distance apart along their entire length; the distance separating them is represented by any of the infinitely many common perpendiculars.

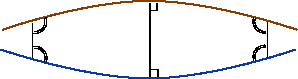
A surface of positive curvature appears (to an ant on the surface) to be bowl-shaped: at every point of the surface it appears to be either a hilltop or the bottom of a bowl, depending on which side of the surface one stands.

Geodesics on a positively curved surface tend to veer towards each other as one moves away from their common perpendicular, which joins the curves at their point of greatest separation.